1. 查找算法分类:
- 静态查找和动态查找;
注:静态或者动态都是针对查找表而言的。动态表指查找表中有删除和插入操作的表。 - 无序查找和有序查找。
无序查找:被查找数列有序无序均可;
有序查找:被查找数列必须为有序数列。
平均查找长度(Average Search Length,ASL):需和指定key进行比较的关键字的个数的期望值,称为查找算法在查找成功时的平均查找长度。
对于含有n个数据元素的查找表,查找成功的平均查找长度为:ASL = Pi*Ci的和。
Pi:查找表中第i个数据元素的概率。
Ci:找到第i个数据元素时已经比较过的次数。
2. 顺序查找
说明:顺序查找适合于存储结构为顺序存储或链接存储的线性表。
基本思想
顺序查找也称为线形查找,属于无序查找算法。从数据结构线形表的一端开始,顺序扫描,依次将扫描到的结点关键字与给定值k相比较,若相等则表示查找成功;若扫描结束仍没有找到关键字等于k的结点,表示查找失败。
复杂度分析
查找成功时的平均查找长度为:(假设每个数据元素的概率相等) ASL = 1/n(1+2+3+…+n) = (n+1)/2 ;当查找不成功时,需要n+1次比较,时间复杂度为O(n); 所以,顺序查找的时间复杂度为O(n)。
代码实现
public int seqSearch(int[] arr,int key) { |
3. 二分查找
说明:元素必须是有序的,如果是无序的则要先进行排序操作。
基本思想
也称为是折半查找,属于有序查找算法。用给定值k先与中间结点的关键字比较,中间结点把线形表分成两个子表,若相等则查找成功;若不相等,再根据k与该中间结点关键字的比较结果确定下一步查找哪个子表,这样递归进行,直到查找到或查找结束发现表中没有这样的结点。
复杂度分析
最坏情况下,关键词比较次数为$log_2(n+1)$,且期望时间复杂度为$O(log_2n)$;
注:折半查找的前提条件是需要有序表顺序存储,对于静态查找表,一次排序后不再变化,折半查找能得到不错的效率。但对于需要频繁执行插入或删除操作的数据集来说,维护有序的排序会带来不小的工作量,那就不建议使用。——《大话数据结构》
代码实现
public class Main { |
4. 插入查找
插入查找其实是从二分查找 优化而来,改变了查找的规则,从而实现快速查找。插值查找算法的mid 是自适应的,而二分查找的 mid 总是 序列的中间值,插入查找的mid = low + (high - low) * (key - arr[low]) / (arr[high] - arr[low]) 。这里的low对应二分查找的left,right对应于二分查找的right,key就是要查找的数字。
$$mid=low+\frac{key-a[low]}{a[high]-a[low]}(high-low)$$
思路同二分查找相同
举例说明: 插值查找算法 查找数组中数值为8的元素下标
代码实现
public class Main { |
5. 斐波那契查找
基本思想
斐波那契查找就是在二分查找的基础上根据斐波那契数列分割的,在斐波那契数列找一个等于略大于待查找表长度的数f(k),待查找表长度扩展为f(k)-1(如果原来数组长度不够f(k)-1,则需要扩展,扩展时候用原待查找表最后一项填充),mid = low + f(k-1) -1,已mid为划分点,将待查找表划分为左边,右边
划分图示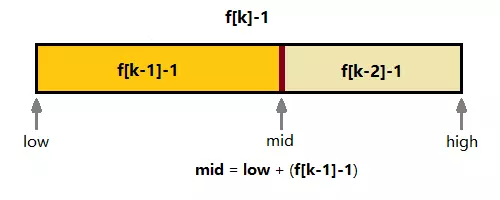
复杂度分析
最坏情况下,时间复杂度为$O(log_2n)$,且其期望复杂度也为$O(log_2n)$。
代码实现
public class Main { |
6. 二叉树查找
基本思想
二叉查找树是先对待查找的数据进行生成树,确保树的左分支的值小于右分支的值,然后在就行和每个节点的父节点比较大小,查找最适合的范围。 这个算法的查找效率很高,但是如果使用这种查找方法要首先创建树。
复杂度分析
它和二分查找一样,插入和查找的时间复杂度均为$O(log_2n)$,但是在最坏的情况下仍然会有O(n)的时间复杂度。原因在于插入和删除元素的时候,树没有保持平衡。
代码实现
class BSTNode<T extends Comparable<T>> { |